相似条件,平行線と線 分の比についての性 質,相似比と面積比及 び体積比の関係を理解 し,知識を身に付けて いる。 4 単元について (1) 教材観 小学校算数科では,第6学年で,図形についての観察や構成などの活動を通して,縮図や拡大図なので、その面積は、 \(2×(\sqrt{3}1)×\displaystyle \frac{1}{2}=\sqrt{3}1(cm^2)\) これが求める答えとなります。 (2)三角形 \(EDC\) の面積の別解 (1)で \(\triangle EDC \backsim \triangle EBA\) を示しています。 この相似比と面積比でも解答可能です。 相似比は、 \(1\sqrt{2}\)・面積比は 32:52=9:25 思考の取り出し 問題 ☆記述のポイント! 思考の深化 「ミックスピザはどっちがお得?」 ~相似比や面積比を利用し,日常生活の疑問を解決する~ ☆本時のねらい:相似な図形の相似比と面積比の関係を理解し,それを

中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
相似比と面積比 証明
相似比と面積比 証明-さらに,相似な図形の相似比と面積比,体積 相似な図形に気付き,相似条件を用いて2つの三角形が相似であることを証明している。また,相似 比を利用して比例式をつくり,その求め方を説明してい本単元では、三角形の相似条件を基に、平行線と比の性質や中点連結定理などの性質を証明する。さらに、 相似比と面積比、 体積比の関係を見いだす。これらの学習を通して、図形の性質について論理的に考察し、 表現する能力を更に伸ばしていく。また、身の回りの事象から相似な図形を見いだし、 図形の性質を用いて考察することで、日常生活とのつながりに気付くことができる。このように基




相似の面積比を求める問題 上級編 Youtube
と相似 ・比と平行線の定理の証明 (6) §2比と平行線 3 ・比と平行線の定理の利用 中点連結定理 形成的評価 1 3相似と §1相似な図形の ・相似な三角形の面積比(本時) 計量 面積比 15 ・相似な図形の面積比 (4) §2相似な立体の表 1 ・相似な立体の表面積比6 相似比と面積比の関係についてま 解することめる。 相似な三角形で m となる 7 シートの問1、問2を解く。 気 Qの結果から言えることを、シートに書かせた 相似な図形の相似比と面積比、それらの関係について理 とができる。<観察・学習シート>の相似条件,平行線と 線分の比についての 性質,相似比と面積比 及び体積比の関係な どを理解し,知識を身 に付けている。 4 単元について (1) 単元について 学習指導要領の第3学年の目標(2)に「図形の相似,円周角と中心角の関係や三平方の定理
1 相似比と面積比・体積比の関係 相似な図形では次のことが成り立つ。 ① 相似な図形の周の長さの比は,相似比に等しい。 ② 相似な図形の面積比は,相似比の2 乗に等しい。 ③ 相似な立体の表面積比は,相似比の2 乗に等しい。 ④ 相似な立体の体積比は相似であることを証明するには「2組」を示せば十分だということ 右図では ∠B=∠Q, ∠C=∠R を示せば, ∠A=∠P は自動的に成り立つ. (2) 「3組の辺の比がそれぞれ等しい」という書き方は2種類ある. ∽ を証明すれば相似の比を使えます。 証明しましょう。 線分の情報がありますが、対応する線分の比を1組しか作れないですね。 そのため「2組の角がそれぞれ等しい」で攻めていきます。 まず共通している角なので、
故に相似な三角形の辺の比は等しくadde=fbbe=13 be=6よりfb=2 線分aeが円oの直径なので、弧aeに対する円周角より∠abe=90°より fbeは直角三角形。 ∴ fbe= 1/2 * fb * be = 6 1 後半 次に fbe gfb = fe fg 2 (fefgが分かれば面積比から gfbの面積を計算できそう・・・)この証明は「相似条件とは?三角形の相似条件はなぜ3つなの?証明問題アリ」の記事でも詳しく解説しております。 スポンサーリンク 平行四辺形を作る 言い忘れてましたが、三角形と比の定理も 全く同じ方法 で証明ができます。 これが、冒頭で「この $2$ つの定理を区別する必要は 三角形の相似条件、記号、相似比・面積比、証明問題 21年2月19日 この記事では、「相似」の意味や記号、三角形の相似条件、相似比と面積比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
相似比の定義 三角形の3 つの相似条件 三角形における平行線と線分の比の関係, 平行線にはさまれた線分の比, 中点連結定理 相似な図形の面積と体積 32 小学校中学校の教科書に関するコメント 1 相似の定義が,小学校と中学校では微妙に異なる.直線相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので ae:de=be:ce=2:3 とわかります。 このae:de=2:3ということを利用して 次は、 adbと edfに注目すると 三平方の定理には数百もの証明方法があります。今回は相似を利用した基本的な証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理
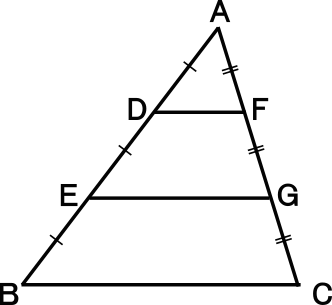



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
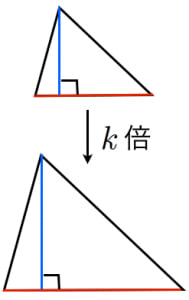
図2 2 2つの三角形の底辺の長さが等しいときは,面積の比は高さの比に等しい. 3 高さが書いていないときでも,1組の辺の比が mn のときは,高さが mn と考えてよい. 2の証明 三角形の面積は(底辺)×(高さ)÷2で求められる.右図の FBC と ABC の面積平行線と比の定理を利用して,図形の性質 を証明することができる。 平行線と比の関係を使って課題解決しよ うとしている。 3 相 似 な 図 形 の ・相似比と面積比の 関係を見つける。 (1) ・面積比や体積比を動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
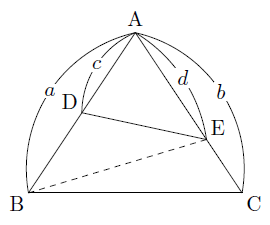



1角共有の三角形の面積比 まなびの学園
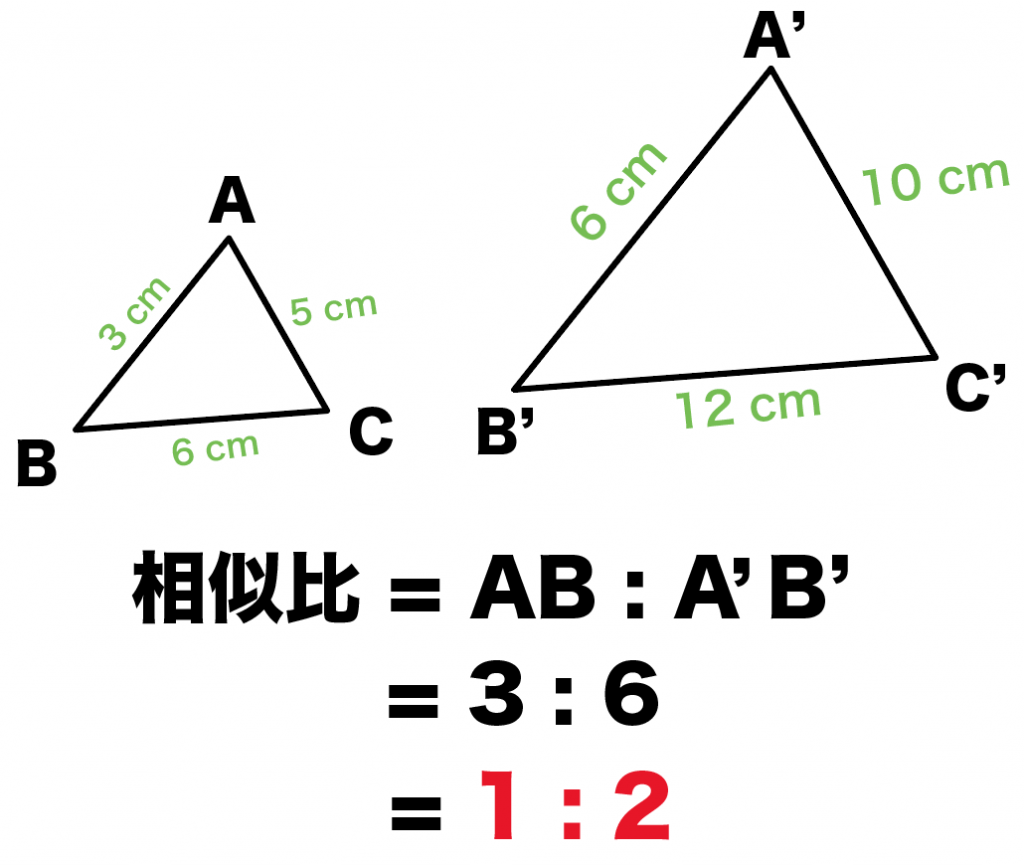



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
・体積比は相似比を ・相似比 (4) ① ② 言語活動③ ・相似比 ・相似比 ま と め る 1 前時の学習事項ついて復習し、本時のめあてを確 認する。 (1) 相似な図形の面積比を振り返る。 ab のとき面積比 大カップが普通のアイスの何倍だったら、クラ 予想 相似比と体積比 相似な図形の体積比の問題です。 基本を確認して、いろいろな応用問題を解けるようにしてください。 基本事項 相似比が a b である図形の面積の比は, a3 b3 である。 *簡単な証明もできるようにしましょう。(1)は線分比が面積比になる性質を使いますが、2回使います。 (2)は線分比が面積比になる性質と相似比が面積比になる性質を使います。 このようなに複数回の比をとるときは整数比を調整します。 それはどういうことか? ab=23 cd=34 ac=45




平面図形の苦手を解消 三角形の面積比 基本編
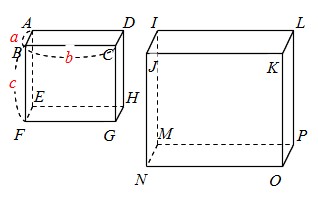



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ
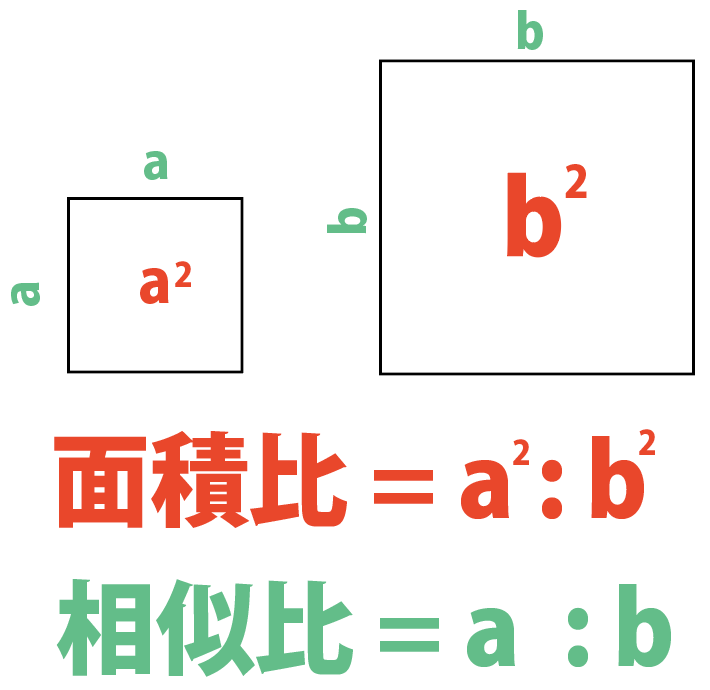
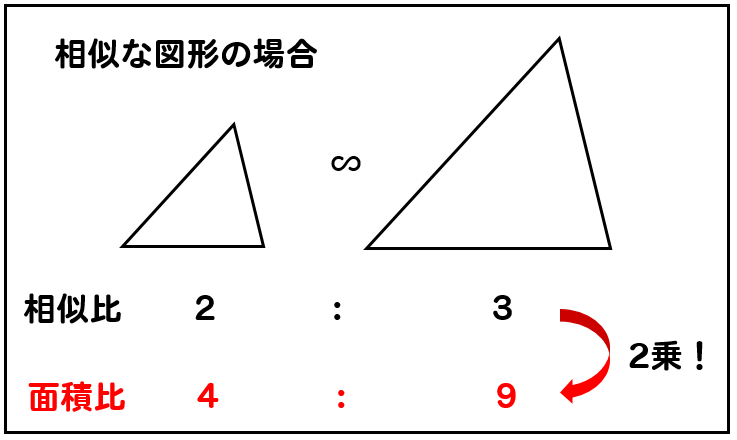
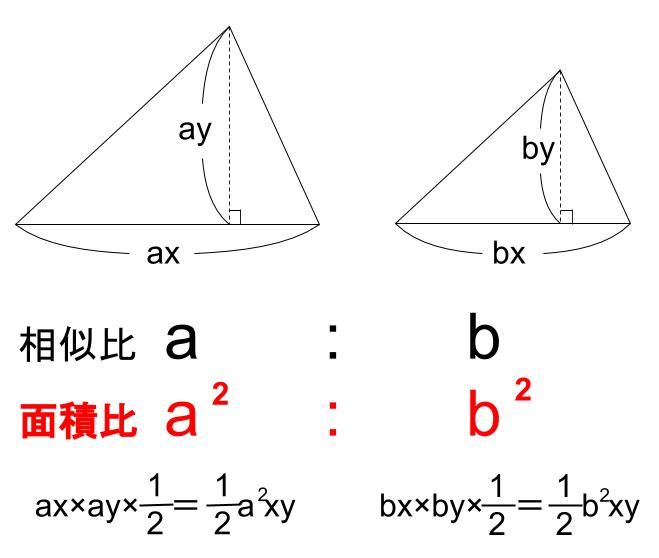
相似な図形の面積比 下の図のような相似な三角形があります。 2つの図形の相似比が\(ab\)のときの面積比は\(a^2b^2\)となります。 相似比の2乗が面積比ということです。 1 相似な図形の面積比は相似比の2乗と覚えておけばいいと思います。相似な空間図形の相似比と面積比,体積比の関係を知り, 使うことができる。 問題 の図ような円錐容器に コップ1杯の水を入れたら, 深さが容器の半分になった。 この容器を満水にするにはあ と何杯必要ですか。 文字を用いて一般的に相 似比と面積 さらに、相似比が1:3であれば、三角形の底辺も高さも3倍になるので面積比は1:9になります。 このことから、多角形について ということが分かります。 相似比から面積比を求める考え方はよく使うので、しっかり理解しておきましょう。 三角形の相似




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



1
2辺の比から面積の比を求める基本問題の逆算パターンです。 「隣辺比」 と呼ばれる解き方です。 右の図のように、 三角形abcと三角形adeで「ひとつの角(角a)が共通(重なっている)」とき、 面積の比はその共通角をはさむ2辺の積、15 相似な三角形や四角形で,相似比と面積比 の関係について説明する。 主 知 16 相似な平面図形の相似比と面積比の関係を 利用して図形の面積を求める。技 17 相似な立体の相似比と表面積の比の関係に ついて説明する。主 思 相似比の2乗の比 になってるのよ。 相似比が12の「円錐A・Bの表面積の比」は、 1^2 2^2 = 1 4 になるわけね。 もし、円錐Bの表面積が40 cm^2だったら、 円錐Aの表面積は10 cm^2 になるわけだね。 おめでとう! 相似比から表面積の比も求められたね! まとめ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
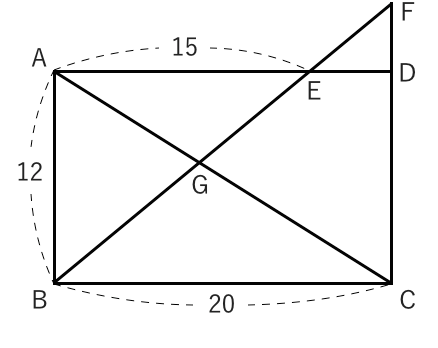



相似な図形 面積比の問題 苦手な数学を簡単に
⑥相似比と面積比の関係や, 相似比と体積比の関係を, 具体的な場面で利用する ことができる。 ①相似な図形の性質 を理解している。 ②三角形の相似条件 を理解している。 ③相似の考えを用い た間接的な高さや 距離の求め方を理 解している。図6のように2つの三角形で1つの角が共通のとき,この角をはさむ2辺の比が各々 ab , mn のとき,面積の比は ambn になる. 図5 4の証明数学・算数 多角形の面積比について 三角形の面積比は相似比の二乗となると思いますが、これは八角形など、どんな多角形にも応用できるのでしょうか? 質問No
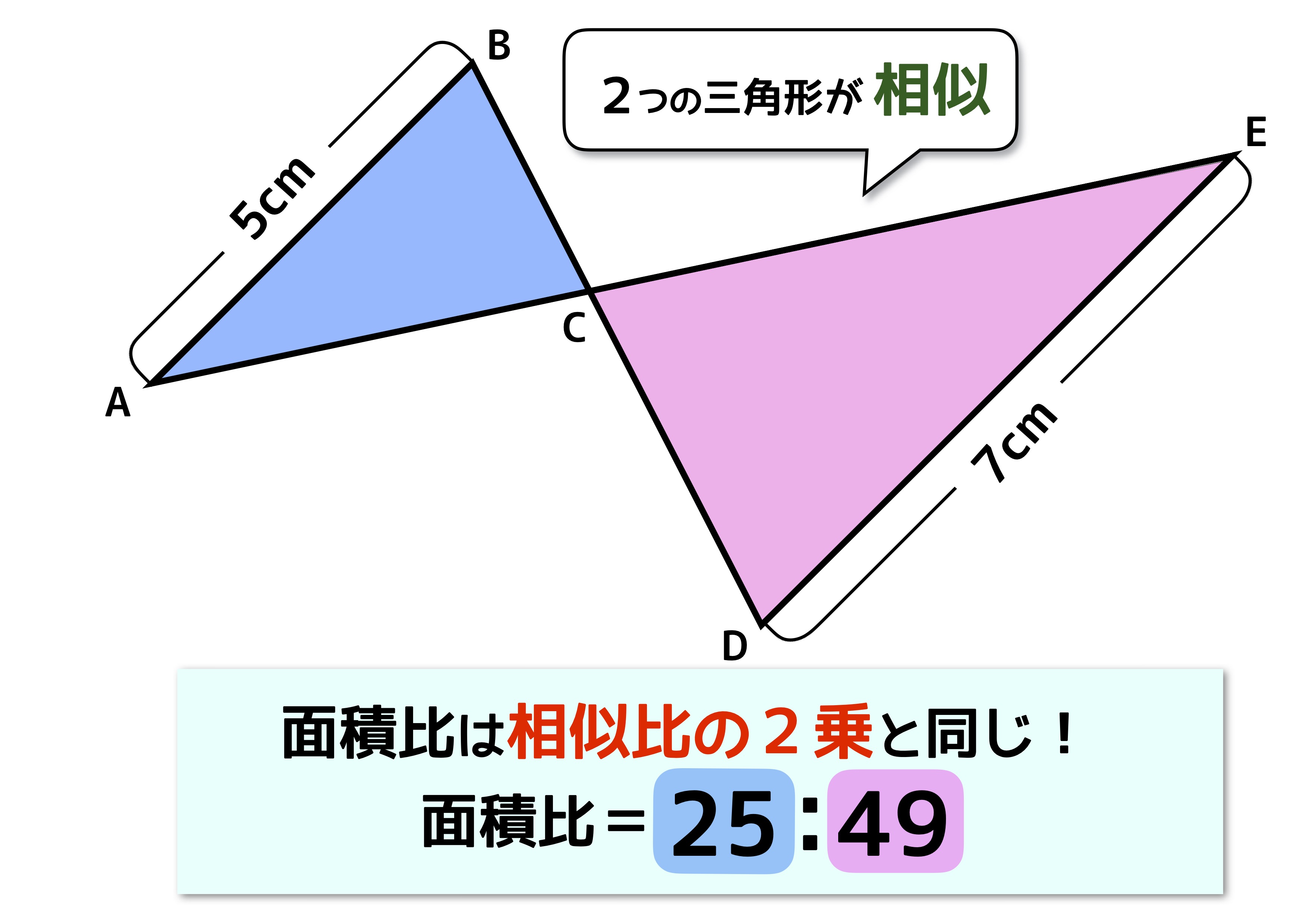



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
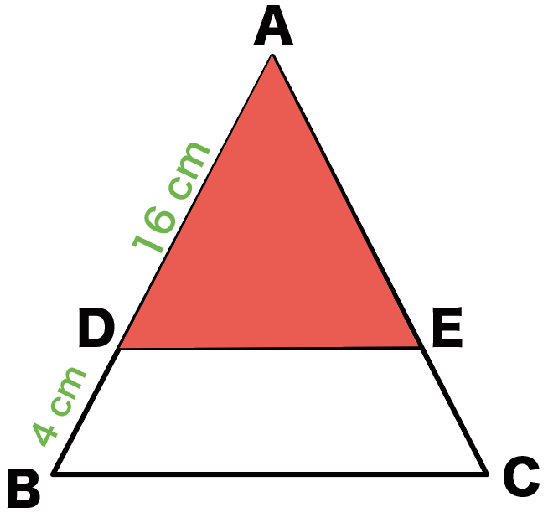



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
相似が言えれば apae の比がわかると面積比もわかる。 apae がわかってもそれでそのまま 2 乗が面積比になるわけではない。 相似がいえて初めて辺の比の 2 乗が面積比になるのでまずは相似を言うこ分の比についての性 質、相似比と面積比及 び体積比の関係を理 解し、知識を身に付け ている。 5.単元の指導計画(全25時間) 1節 図形と相似 1 相似な図形 3時間 2 三角形の相似条件 2時間 3 相似条件と証明(本時3/3) 3時間
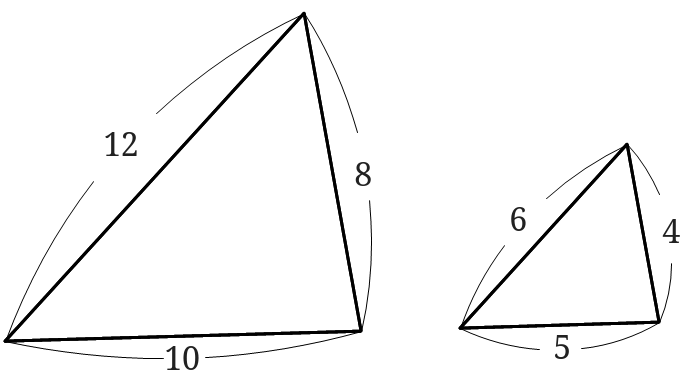



相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局
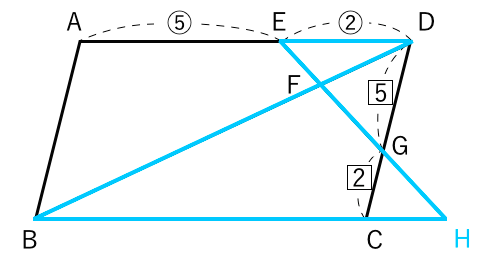



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局




中学校数学 証明のコツ 面積比 体積比
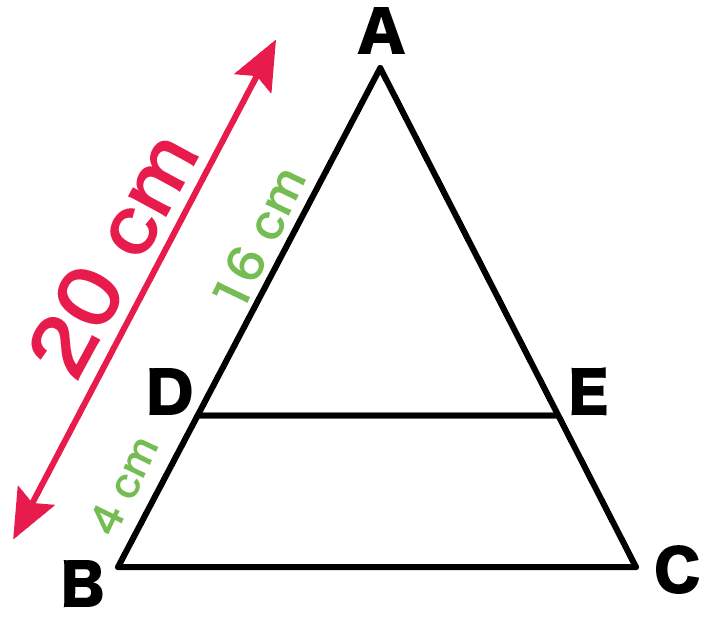



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
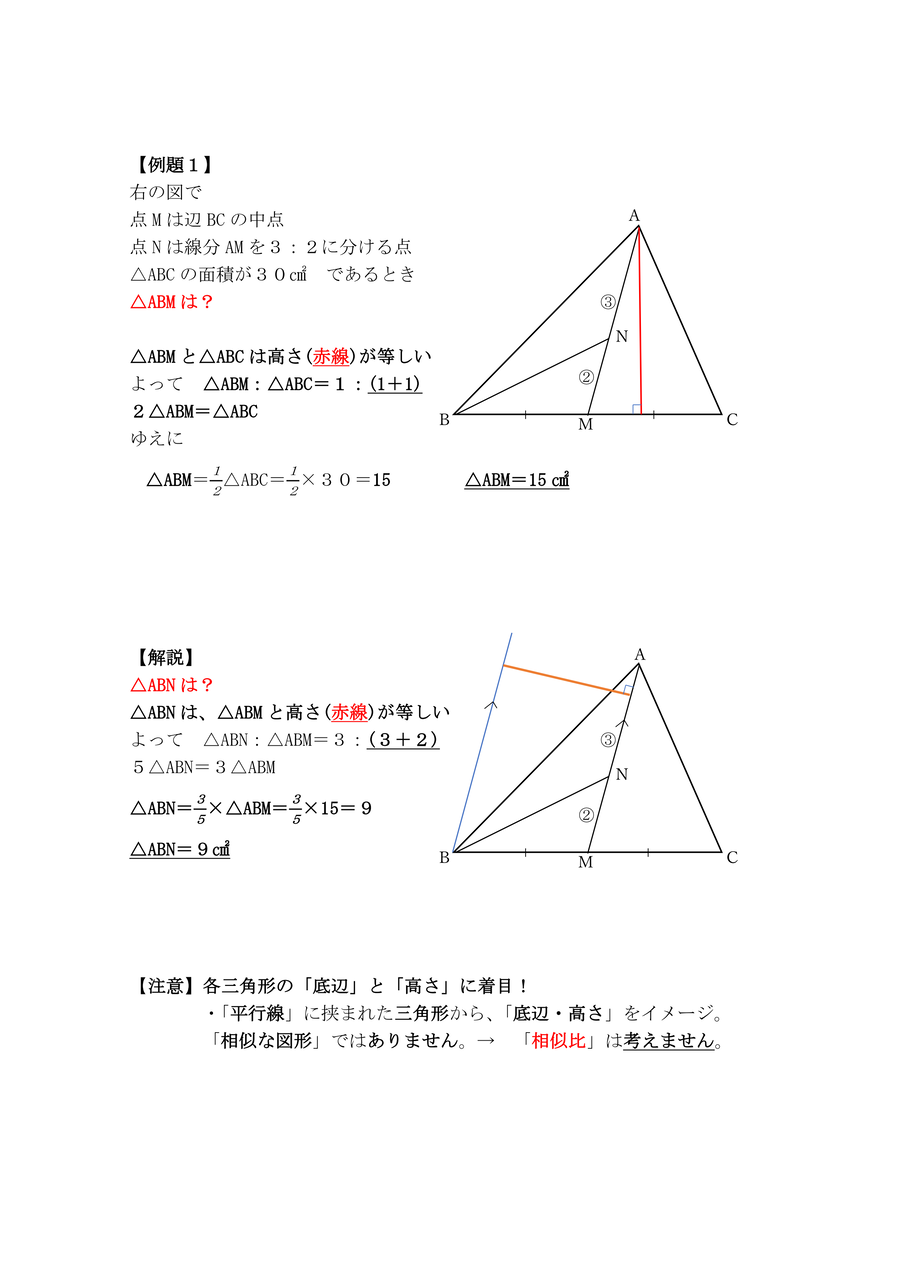



中学校数学 証明のコツ 面積比 体積比



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



相似比と面積比 体積比の公式の証明 高校数学の美しい物語
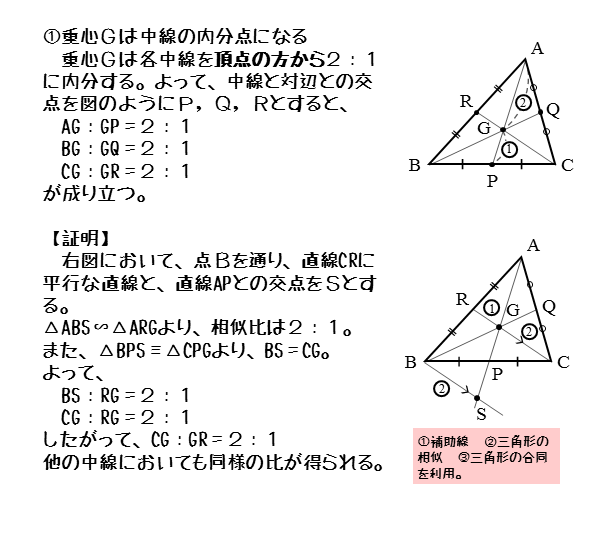



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
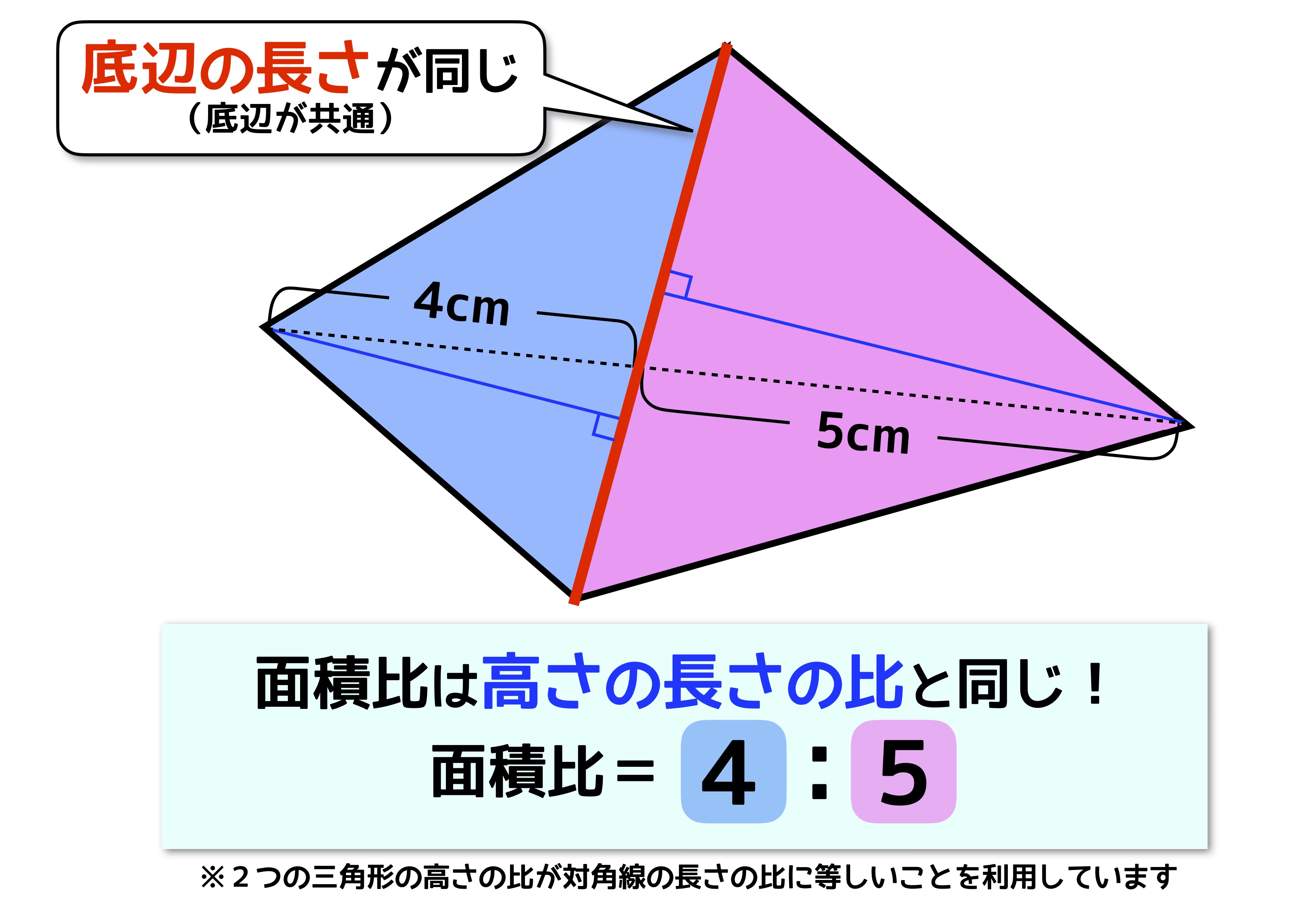



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



3
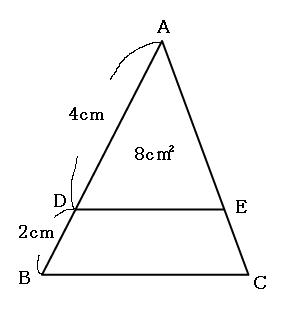



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




相似の面積比を求める問題 上級編 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




相似 台形と面積比の問題を徹底解説 数スタ




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
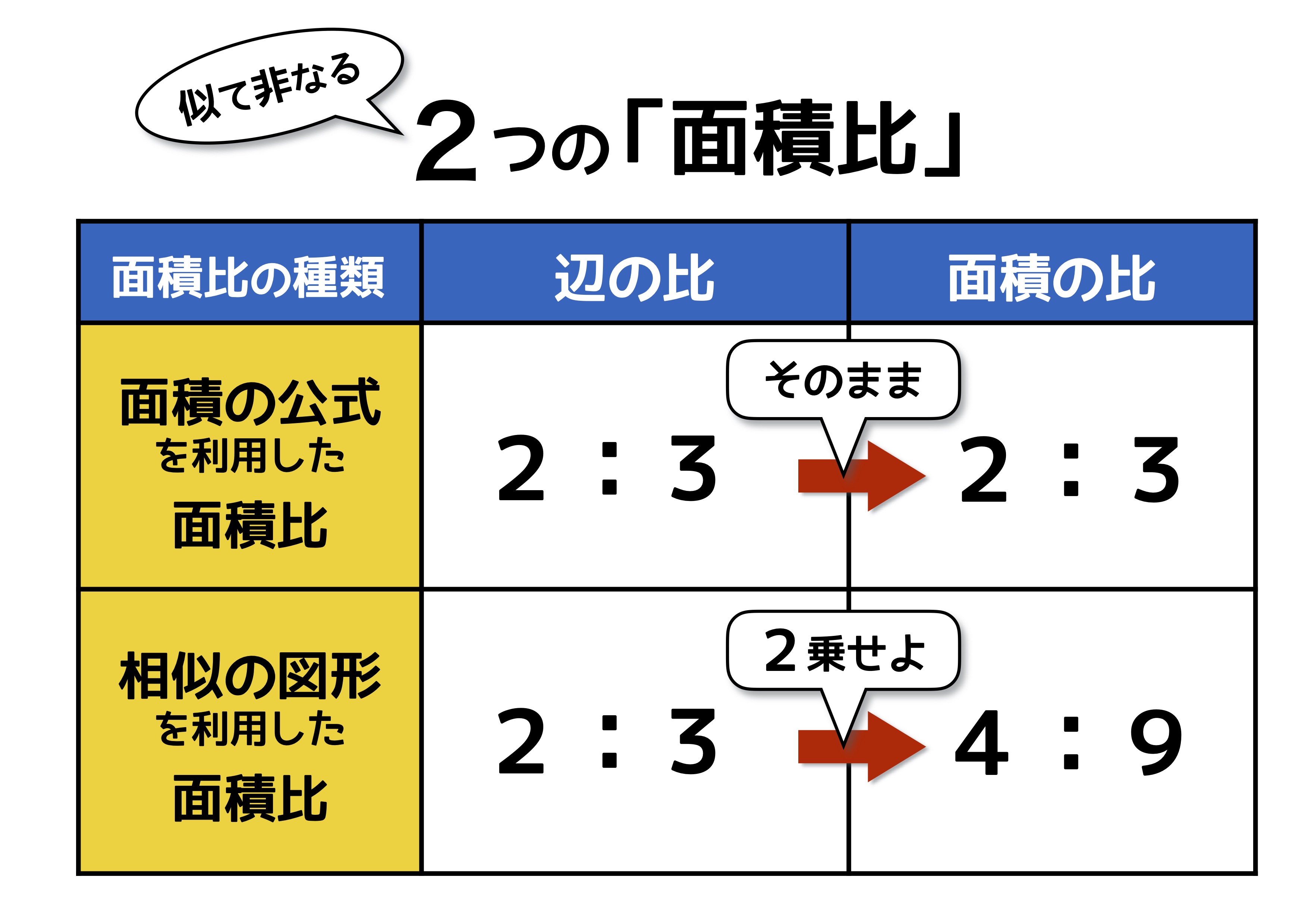



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
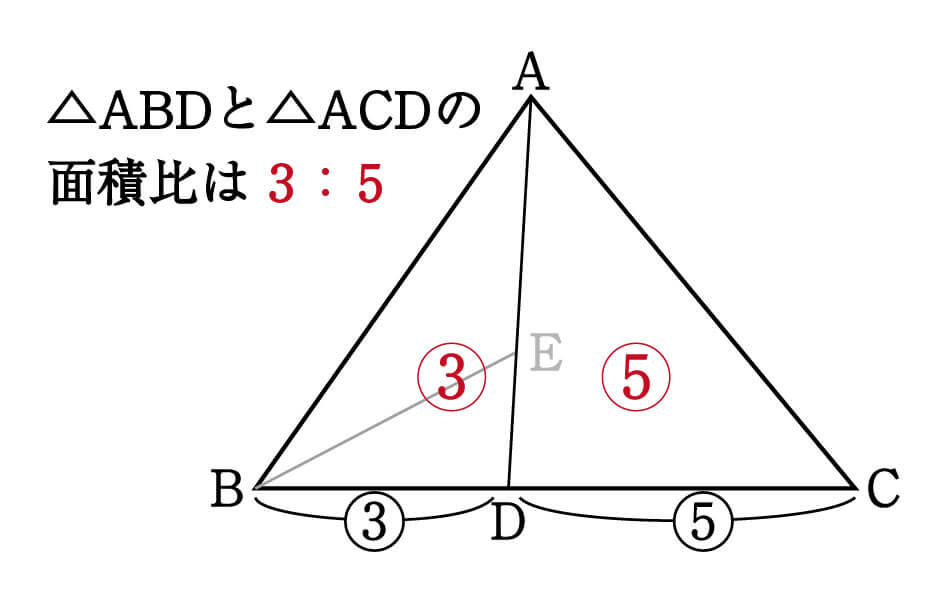



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
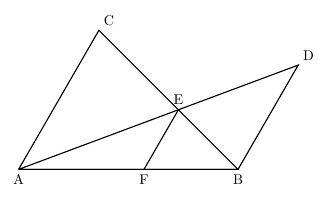



線分比と面積比の問題の解法 夢を叶える塾




高校入試対策数学 面積比に関する対策問題 Pikuu




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
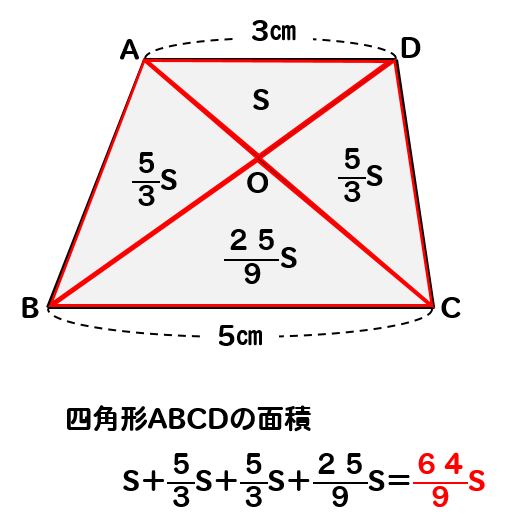



相似 台形と面積比の問題を徹底解説 数スタ



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ The 2nd



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



相似比と面積比 中学から数学だいすき




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




数学 中3 53 相似と面積 応用編 Youtube



なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく




中学数学 相似じゃない面積比 平面図形 Youtube
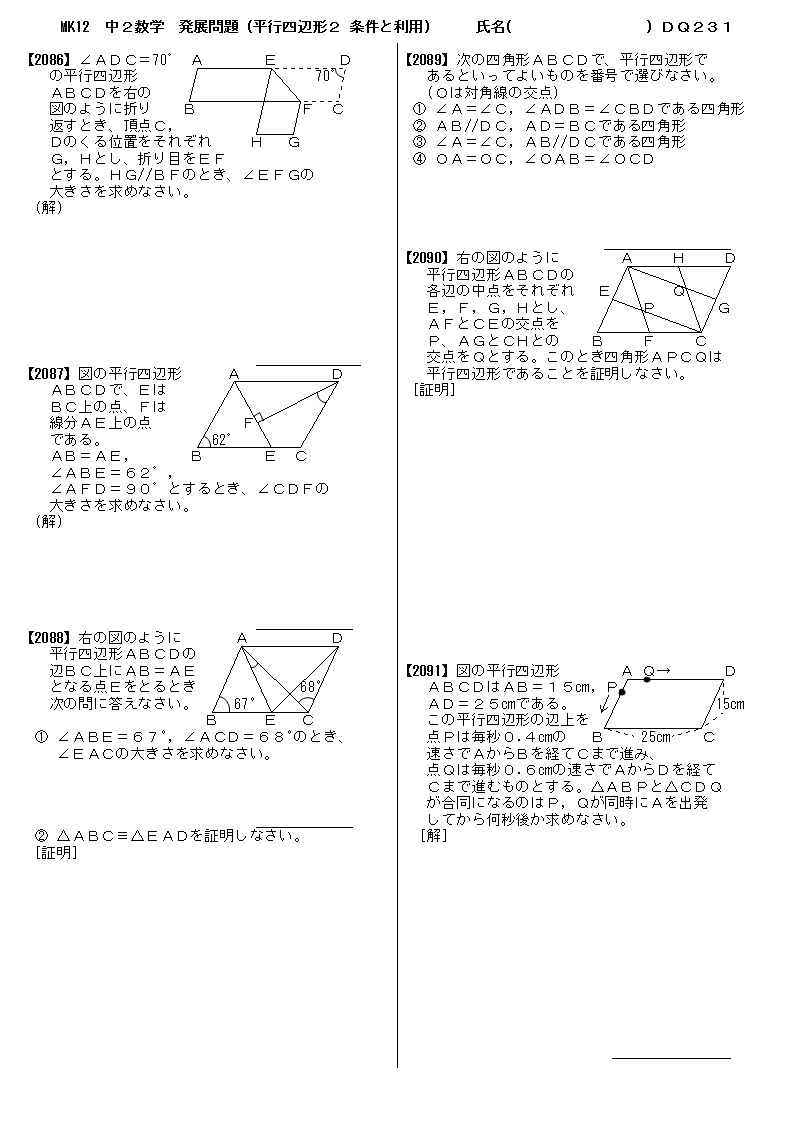



無料 中2数学 応用 発展問題 問題プリント 331 図形の相似6 面積比 体積比




相似比を使って辺の長さを求める Youtube
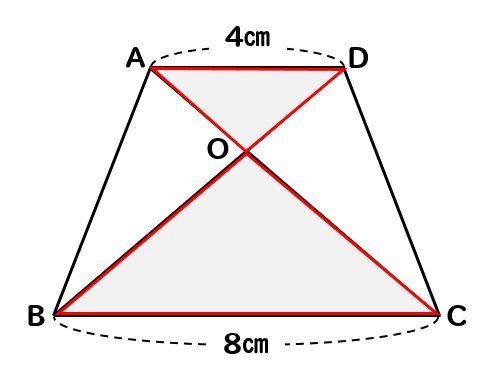



相似 台形と面積比の問題を徹底解説 数スタ



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題



面積比 体積比



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題
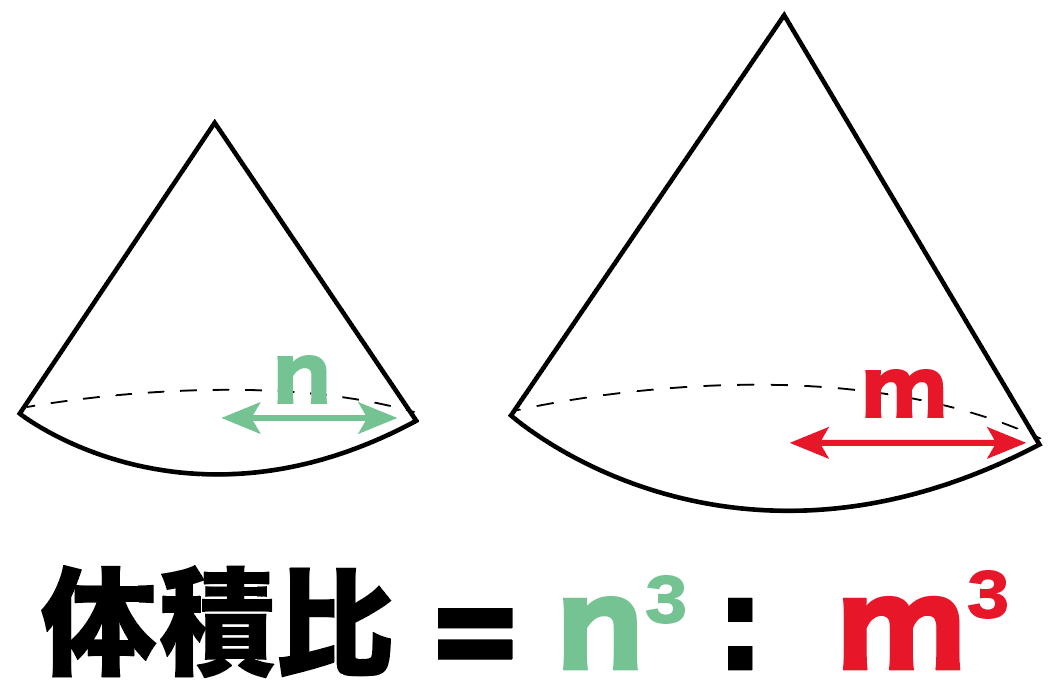



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




相似比と面積比 中学3年数学 Youtube
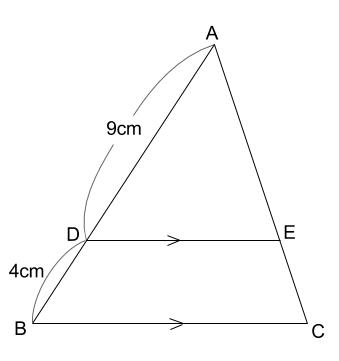



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




大至急です 相似 面積比の問題です Clear
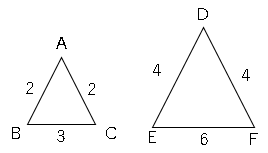



相似な図形の面積比と表面積と体積の関係 数学の要点まとめ 練習問題一覧
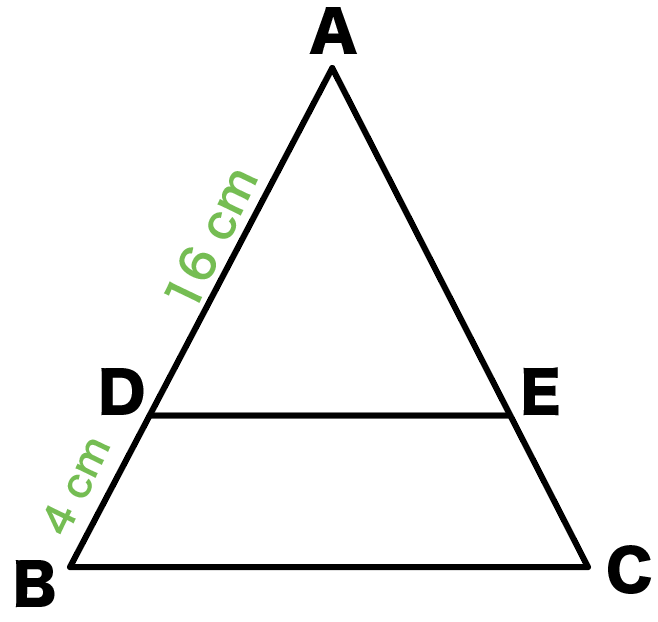



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



相似比と面積比 中学から数学だいすき




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




相似比と面積比 中学3年数学 Youtube



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor
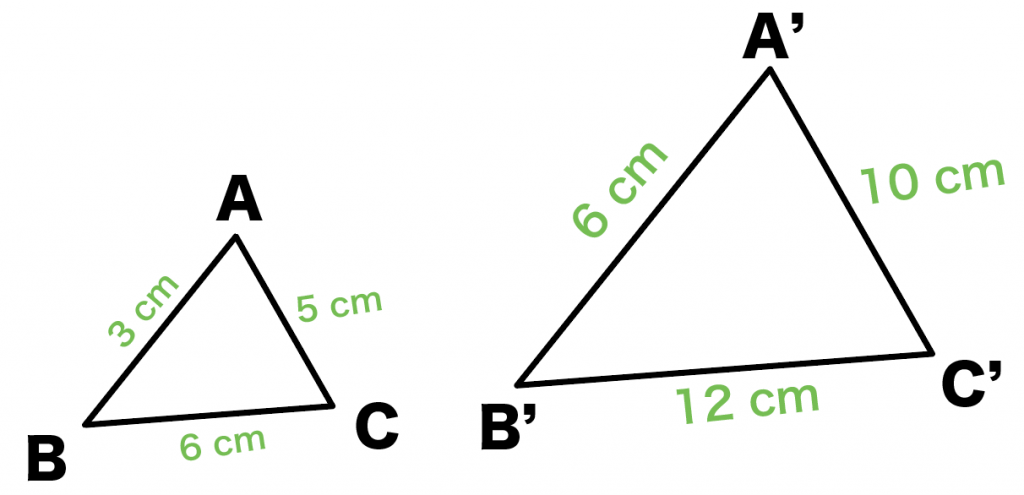



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
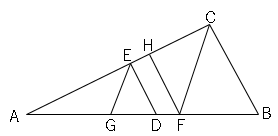



辺の比と三角形の面積比と証明問題 数学の要点まとめ 練習問題一覧




平面図形をマスター 三角形の面積比 応用編その3



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




平面図形の苦手を解消 三角形の面積比 基本編



相似 台形と面積比の問題を徹底解説 数スタ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
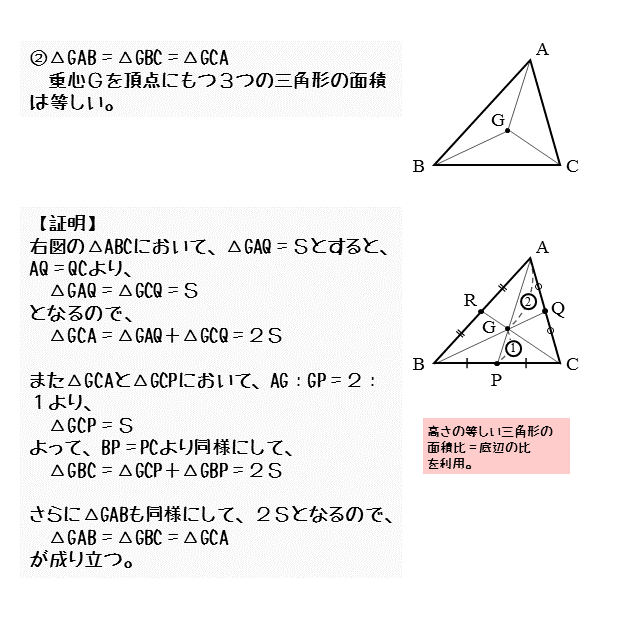



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



3
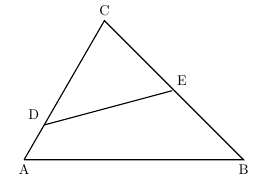



相似の証明の問題の解法 夢を叶える塾



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




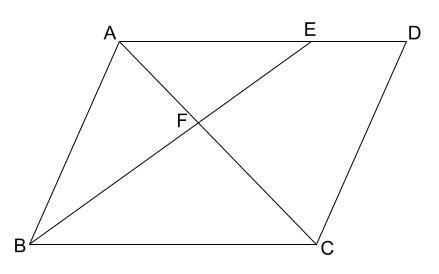
中3 19 2 平行四辺形と相似 Youtube



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



1




辺の比と面積比問題 考え方1 Youtube
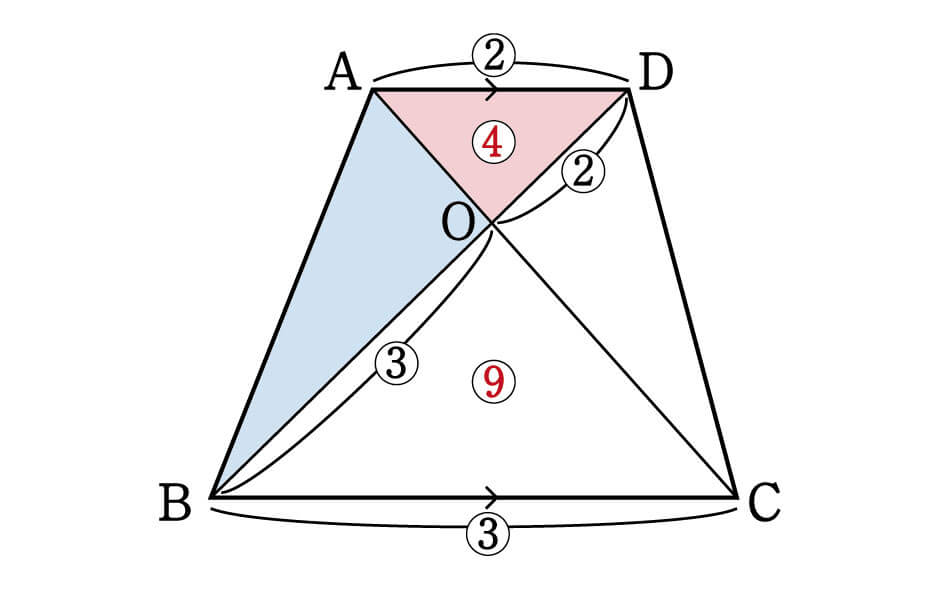



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




相似じゃない三角形の面積比の求め方がよく分かりません Clear




平面図形の苦手を解消 三角形の面積比 基本編



Studydoctor台形の面積比 中学3年数学 Studydoctor




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ




相似比と面積比 1 Abdの周の長さを求めてください 2 Ab Okwave



数学 相似な図形では面積比は相似比の二乗に等しくなる の証明をしてい Yahoo 知恵袋




17年11月29日 数学 円周角の定理 相似比を使った面積比と体積比 相似の証明 オンライン家庭教師 ウェブリー




相似比と面積比 体積比の公式の証明 高校数学の美しい物語



高校入試 英語 数学 図形と相似 面積比と体積比




補助線の引き方 日々の学習 兄中学受験




17年11月29日 数学 円周角の定理 相似比を使った面積比と体積比 相似の証明 オンライン家庭教師 ウェブリー




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
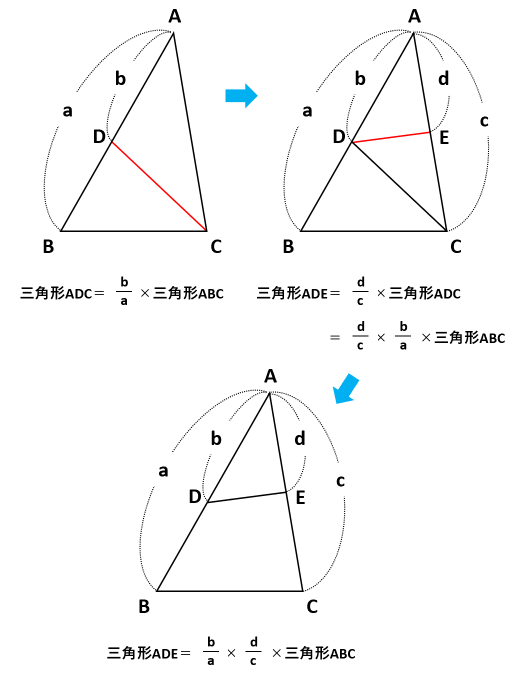



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




中3 三角形の相似 円錐の体積比 日本語版 Youtube




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



0 件のコメント:
コメントを投稿